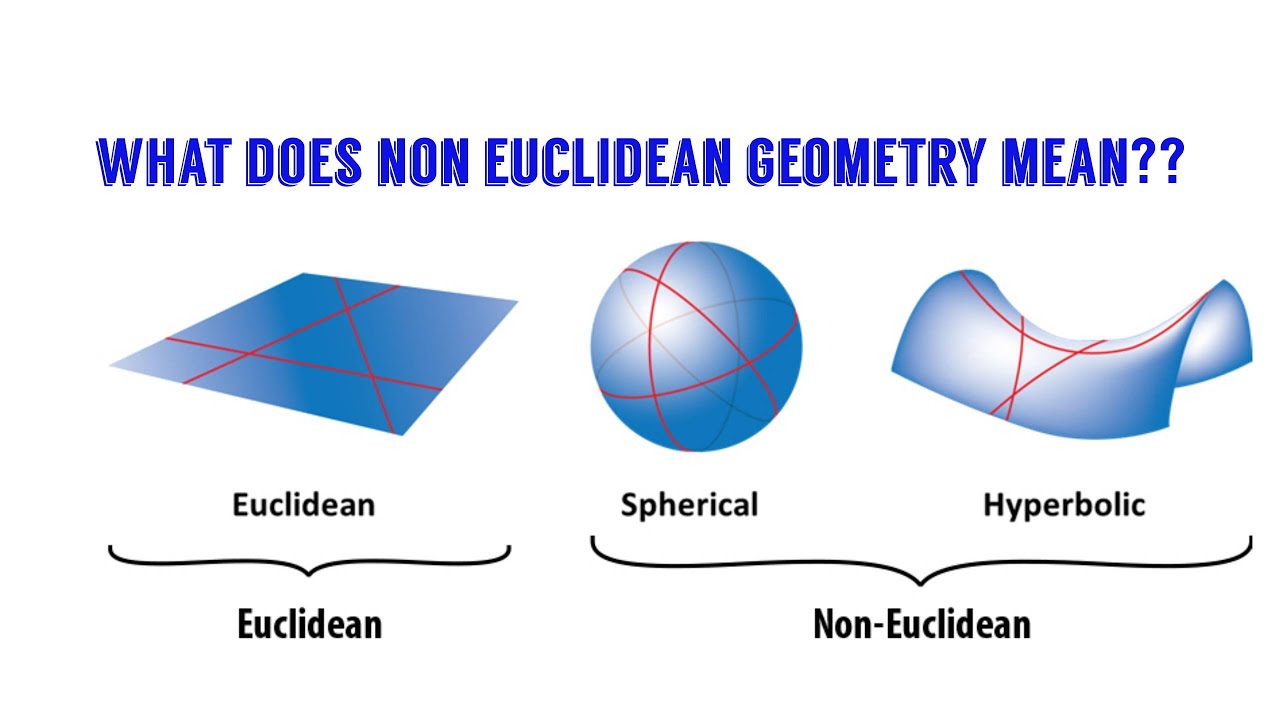
Mathematics is a branch of knowledge that studies structures, numerical relationships, spatial configurations, and other abstract concepts. One of the most important branches of geometry is the distinction between Euclidean and non-Euclidean geometry, which differ significantly in their foundations.
While Euclidean geometry seeks to understand the geometry of flat two-dimensional spaces, non-Euclidean geometry studies curved rather than flat surfaces. While Euclidean geometry is useful in many fields, in some cases, non-Euclidean geometry may be more useful.
Euclidean geometry
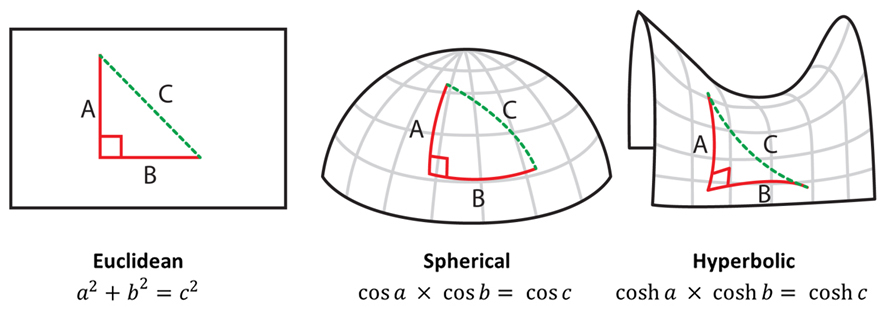
Euclidean geometry is a classical geometry developed by the ancient Greek scientist Euclid in the third century BC. It is based on five basic axioms from which all the theorems and statements of this geometry are derived. The main feature of Euclidean geometry is the concept of a “plane” or “space” in which the following basic principles apply:
- A straight line: Only one line can be drawn through any two points.
- Parallelism: If a line that intersects two other lines makes right angles with them, then the two lines are parallel and do not intersect.
- Distance and angles: The distances between points and the angles between lines are defined in a certain way, which allows you to accurately measure objects in space.
All traditional results of geometry, particularly in the plane (e.g., properties of triangles, circles, lines), are related to Euclidean geometry. It is used in the classical sciences, architecture, and engineering.
Non-Euclidean geometry
Non-Euclidean geometry is a geometry that emerged as an alternative to Euclidean geometry in the mid-nineteenth century, when mathematicians Carl Friedrich Gauss, Jacob Benedict Beaulieu, and Nikolai Lobachevsky began to develop theories of geometry where the axiom of parallel lines does not necessarily hold.
There are two main areas of non-Euclidean geometry:
- Gauss-Bohlai-Lobachevsky geometry: Here the axiom about parallel lines is modified. In this geometry, infinitely many lines can be drawn through a point that do not intersect a given line (i.e., are parallel). This type of geometry is often called “negative curvature geometry”.
- Riemannian geometry: It is based on the assumption that instead of a flat space, we have a “spherical” space where only one line can be drawn through any two points, and all lines (in general, large circles on a sphere) eventually intersect. This geometry is known as “positive curvature geometry”.
Non-Euclidean geometries are important in physics, especially in relativity, where the concept of curved space is used.
Conclusion
The difference between Euclidean and non-Euclidean geometry lies in the basic assumptions about parallel lines. Euclidean geometry describes a regular “flat” space where parallel lines do not intersect, while non-Euclidean geometries introduce new ways of interpreting space and parallel lines, which opens up new possibilities for studying complex mathematical and physical phenomena.