Інтеграли — це один з основних інструментів в математичному аналізі, який дозволяє знаходити величини, що описують різні процеси в природі та техніці. Вони є зворотними операціями до похідних, і часто використовуються для розв’язання задач на площі, об’єми, а також для розрахунків у фізиці, економіці та інженерії. Замість того, щоб вивчати, як швидко змінюється функція, інтеграли дозволяють визначити, який результат виходить після “накопичення” цих змін. У цьому дописі ми розглянемо основи інтегралів, їх типи та приклади практичного застосування.
Що таке інтеграл?
Інтеграл — це математичне поняття, яке описує загальну величину, отриману в результаті певного процесу, наприклад, нахилу кривої або площі під графіком функції. Якщо похідна дає нам швидкість зміни величини, то інтеграл дозволяє знайти сумарний результат цих змін.
Існують два основні типи інтегралів: неозначені та означені.
1. Неозначений інтеграл
Неозначений інтеграл функції f(x) — це операція, яка дає родину функцій, похідні яких дорівнюють f(x). Неозначений інтеграл позначається так:

2. Означений інтеграл
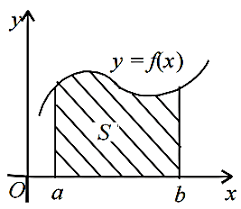
Означений інтеграл використовується для знаходження конкретного значення площі під графіком функції між двома точками на осі x. Це числове значення, яке визначається через межі інтегрування:

Застосування інтегралів:
- Площі та об’єми: Інтеграли широко застосовуються для обчислення площі під кривими, а також об’ємів твердих тіл.
- Фізика: У фізиці інтеграли використовуються для визначення роботи, енергії, швидкості та інших важливих величин.
- Економіка: В економіці інтеграли застосовуються для розрахунку накопичених величин, таких як загальний дохід або витрати протягом певного періоду.
Інтеграли є важливим інструментом для вирішення практичних задач, що потребують точних обчислень та моделей, і знаходять застосування в багатьох сферах науки і техніки.